- 2.2.4 Hypergeometrische Verteilung
Die hypergeometrische Verteilung gehört zu den wichtigen diskreten Wahrscheinlichkeitsverteilungen. Von besonderer Bedeutung ist sie wie die Binomialverteilung bei Bernoulli-Experimenten, d.h. wenn die Zufallsvariablen genau zwei sich ausschließende Ausprägungen besitzen. Die hypergeometrische Verteilung ist bei Stichprobenentnahmen ohne Zurücklegen anzuwenden, beispielsweise bei der Qualitätssicherung in der Produktion.
- Beispiel 1:
Aus einer Urne mit 5 roten und 10 weißen Kugeln wird eine Kugel gezogen, danach wird das Experiment n mal wiederholt. Die entnommene Stichprobe ist hypergeometrisch verteilt, da die Kugeln nicht wieder zurückgelegt werden: „Ziehen ohne Zurücklegen“. Auch die Wahrscheinlichkeit beim Lotto mit 6 aus 49 Zahlen Gewinne zu machen ist hypergeometrisch verteilt.
- Ursprung:
Die Grundlagen der hypergeometrischen Verteilung gehen auf die Arbeiten von Blaise Pascal und Jakob I. Bernoulli zurück.
- Charakteristik:
Die hypergeometrische Verteilung gibt den Zusammenhang an zwischen der Anzahl mit einem Merkmal behafteten Einheiten in einer Stichprobe (z.B. Fehler, i,O, usw.) und der zugehörigen Wahrscheinlichkeit der Auftretens dieser Eigenschaft in einer Stichprobe vom Umfang n.
- Die entnommene Stichprobe wird nach Beurteilung nicht wieder zurückgelegt: „Ziehen ohne Zurücklegen“
- 2.2.4.1 Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung
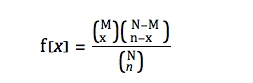
- M = Zahl der Erfolge
- N = Grundgesamtheit
- n = Größe der Stichprobe
- x = gesuchter Wert der Erfolge (ganzzahlig)
- 2.2.4.2 Lageparameter und Approximation
- Erwartungswert E(x) = n M/N = np
- Varianz Var(x) = n p (1 - p) ((N - n)/(N - 1)) mit p = M/N
- Für n < N/10 wird die hypergeometrische Verteilung gut durch die Binomialverteilung approximiert
- Funktionsbezeichnung in Excel: HYPGEOMVERT
- 2.2.4.3 Übungsaufgaben
- 6. Rechnen mit Binomialkoeffizienten und Hypergeometrische Verteilung (I)
In einem Karton liegen 80 Bauteile, davon sind 5 nicht funktionsfähig. Wie groß ist die Wahrscheinlichkeit bei drei mal Ziehen ohne Zurücklegen:
a.) kein fehlerhaftes Teil zu erhalten?
b.) genau ein Fehlerteil zu erhalten?
c.) drei nicht funktionsfähige Teile zu erhalten?
- 7. Rechnen mit Binomialkoeffizienten und Hypergeometrische Verteilung (II)
In einer Geldbörse sind 15 Geldscheine, davon sind 5 gefälscht. Es wird eine Stichprobe von n=3 gezogen (ohne Zurücklegen). Wie groß ist die Wahrscheinlichkeit:
a.) keinen gefälschten Geldschein zu finden?
b.) Genau einen gefälschten Geldschein zu finden?
- Lösungen werden im Rahmen der Vorlesung besprochen.